검색결과 리스트
글

Screenshot, Mandelbrot Set program made by me
만델브로트 집합: zn+1 = zn2 + c (z는 복소수, z0= c, n >= 0) 일 때, zinfinity의 크기가 특정 값 이하로 수렴하는 복소수 c의 집합. 보통 |zinfinity| <= 2 를 만족하는 c의 집합.
Mandelbrot set is the set of all complex numbers z for which sequence defined by the iteration "zn+1 = zn2 + c (z is complex number, z0= c, n >= 0)" remains bounded.
Mandelbrot set is the set of all complex numbers z for which sequence defined by the iteration "zn+1 = zn2 + c (z is complex number, z0= c, n >= 0)" remains bounded.
저의 학사 논문 주제입니다. "MPI를 이용한 Mandelbrot set 계산"이 아마 제목이었던 것 같습니다. 학사 논문을 뭘 써야 할까 고민하다가 fractal graphic과 분산 컴퓨팅에 관심이 있어서 두개를 결합하여 프로그램을 작성하게 되었습니다.
카오스 이론이라는 책으로 처음 접하게 된 프랙탈 그래픽. 확대해도 확대해도 자기 자신과 같은 모양이 또다시 나오는 자기 복제성. 그 아름다운 무늬에 마냥 신기했습니다. 그러다가 나중에 만델브로트 집합이 저리도 간단한 식으로 계산된다는 것에 또한 놀라게 되었습니다. 무조건 어려울 줄 알았는데 말이죠. 혼돈 속에 질서가 있고 유한 속에 무한이 있는 프랙탈 그래픽.
지금 보니 만델브로트 셋의 가장 큰 부분 모양이 하트모양이네요. ^^ cardioid라고 하죠. 역시 모든게 연결되나 봅니다. ^^
그 당시에 python을 이용한 분산 환경(MPI)을 구축하여 이미지를 그린 모습입니다. 영역을 지정하면 무한 확대도 되었다죠. C로 작성한 것보다는 무척 느렸지만, 쉽게 MPI를 느껴 볼 수 있는 방법인 것 같습니다. 3년정도 지났는데, 지금은 훨씬 발전해 있겠죠? ^^
다음에 심심할 때 만델브로트 집합 프로그램 업그레이드나 한번 해볼까 막연히 생각해 봅니다. 예쁜 색도 넣고, 더 빠르게도 만들고.. ^^
http://mathworld.wolfram.com/MandelbrotSet.html
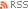
RECENT COMMENT